竹内薫「はじめての数式処理ソフト―Maximaで楽しむ数式計算と物理グラフィック」の中の、平面図が正方形で、正面図が円で、右側面図も円の立体に関する問題。
そこに「Maximaでは複数の3次元グラフを重ねられない」とある。
——ほんと?
と思ったのも、本の中ではgnuplotで図を描いているのだけど、それって変じゃね? と思ったからだ。Maximaもgnuplotで描いているんだから描けそうな気がする。どうなんだろ?
「平面図が正方形で、正面図が円で、右側面図も円」ということは横から見ると、正方形の円柱を寝転がして二個、90度ちがいで重ねれば、よいような……でもそもそも円柱ってどうやれば、いいんだろ?
まずは円か。
これはいちおう、描ける。
plot2d([parametric,cos(t),sin(t),[t,0,2*%pi]],same_xy)$
で、これに高さを与えれば、いいんだから……こうですかね?
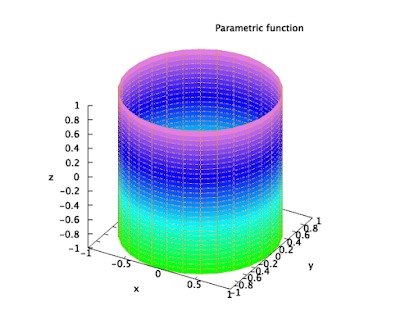
plot3d([cos(t),sin(t),h],[t,0,2*%pi],[h,-1,1],same_xy)$
で、これを転がす、と。
plot3d([h,cos(t),sin(t)],[t,0,2*%pi],[h,-1,1],same_xy)$
さらにこれを90度、ずらして二個、描くと。
plot3d([[h,cos(t),sin(t)],[t,0,2*%pi],[h,-1,1],[cos(t),h,sin(t)],[t,0,2*%pi],[h,-1,1]],same_xy)$
——えっ?
やっぱ、3次元グラフを重ねて描けるじゃないか。
まぁ、10年前の本だから当時は描けなかったのかもしれないけれど。
平面図
正面図
——このはみ出ているところを削ることができれば、答えなんだけどなぁ。これはどうすれば、いいんだろう? まぁ、とりあえず、3次元グラフを重ねられるのなら「はじめての数式処理ソフト―Maximaで楽しむ数式計算と物理グラフィック」のgnuplotのプログラムもmaximaできっと書けるんじゃね?
こうかな?
f(z,t):=t*sqrt(1.0-z^2); plot3d([[f(-0.9,u),f(-0.9,v),-0.9],[u,-1,1],[v,-1,1], [f(-0.8,u),f(-0.8,v),-0.8],[u,-1,1],[v,-1,1], [f(-0.7,u),f(-0.7,v),-0.7],[u,-1,1],[v,-1,1], [f(-0.6,u),f(-0.6,v),-0.6],[u,-1,1],[v,-1,1], [f(-0.5,u),f(-0.5,v),-0.5],[u,-1,1],[v,-1,1], [f(-0.4,u),f(-0.4,v),-0.4],[u,-1,1],[v,-1,1], [f(-0.3,u),f(-0.3,v),-0.3],[u,-1,1],[v,-1,1], [f(-0.2,u),f(-0.2,v),-0.2],[u,-1,1],[v,-1,1], [f(-0.1,u),f(-0.1,v),-0.1],[u,-1,1],[v,-1,1], [f(-0.0,u),f(-0.0,v),-0.0],[u,-1,1],[v,-1,1], [f(0.9,u),f(0.9,v),0.9],[u,-1,1],[v,-1,1], [f(0.8,u),f(0.8,v),0.8],[u,-1,1],[v,-1,1], [f(0.7,u),f(0.7,v),0.7],[u,-1,1],[v,-1,1], [f(0.6,u),f(0.6,v),0.6],[u,-1,1],[v,-1,1], [f(0.5,u),f(0.5,v),0.5],[u,-1,1],[v,-1,1], [f(0.4,u),f(0.4,v),0.4],[u,-1,1],[v,-1,1], [f(0.3,u),f(0.3,v),0.3],[u,-1,1],[v,-1,1], [f(0.2,u),f(0.2,v),0.2],[u,-1,1],[v,-1,1], [f(0.1,u),f(0.1,v),0.1],[u,-1,1],[v,-1,1], [f(0.0,u),f(0.0,v),0.0],[u,-1,1],[v,-1,1], [f(u,1),f(u,1),u],[u,-1,1],[v,-1,1], [f(u,1),f(u,-1),u],[u,-1,1],[v,-1,1], [f(v,-1),f(v,1),v],[u,-1,1],[v,-1,1], [f(v,-1),f(v,-1),v],[u,-1,1],[v,-1,1]])$
あかん、むっちゃ、重い。